6. Group assignment: Analysis of flow past backward facing step by using realizable k-epsilon turbulence model

The project is aimed at the investigation of flow pattern past a backward facing step of variable (a) top wall angle. Results are to be compared with experimental data.

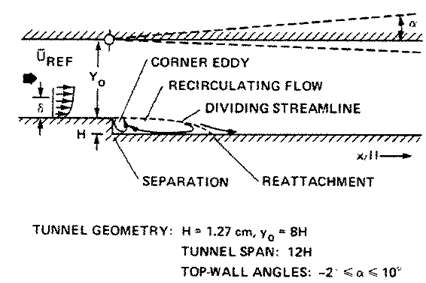
Figure 1. Geometrical model and flow structures.

The backward facing step is located at the lower wall of a channel. The channel has an even width in the direction perpendicular to the x-y plane, that is, a two-dimensional flow can be assumed. The channel height is Y₀(=8H) on the upstream side and Y₀+H on the downstream side of the step; the step height is H. Since each dimension can be expressed in terms of H, only H=12.7mm is specified. The origin of the coordinate system (x=0, y=0) is specified by the upper corner of the step, the inlet is located at x=-2H. The outlet cross-section is at 15H away from the step. The upper wall can be tilted about a turning point just above the step. In this way, the channel can shrink or expand in steamwise direction creating a positive or negative pressure gradient. Angle a is measured between the upper (tilted) wall and the initial flow direction.

Boundary conditions

Velocity and turbulence characteristics are imposed at the inlet boundary according to bfs_belepes.prof. It is important to note, that inlet quantities are specified at x=-2H (upstream from the step), therefore the geometrical model need to be prepared correspondingly. Turbulent kinetic energy (k), turbulent dissipation rate (epsilon) and specific dissipation rate (omega) are contained by the profile file. Use pressure boundary condition at the outlet, and no-slip condition on solid walls.

The reference velocity used in the evaluation of dimensionless quantities is Uref=44.2m/s . Note that, this is not a boundary condition!

Task 1. (3 points)

Preparation of the geometrical model with alfa=-2°, 0°, 6° and 10°;

Generation of block structured mesh;

Please mind that:

- the boundary layers on solid walls, require a proper wall-normal resolution;

- and the shear layer, separated from the upper edge of the step, also needs refinements.

Task 2. (3 points)

Selection and parameterization of boundary condition in FLUENT;

Use the given inlet profile for specifying inlet boundary conditions!

Task 3. (3 points)

Check your mesh for meeting turbulence model criteria as well as resolution required at highly sheared zones for alfa=0 lid angle:

- check if the value of y+ is within the range required by the turbulence model; if not, modify your mesh accordingly;

- perform adaptive refinement in the vicinity of the shear layer and evaluate changes in flow characteristics.

Task 4. (3 points)

Run simulations with realizable k-epsilon turbulence model for 4 different alfa angle!

- Plot velocity profiles downstream from the step in 1H, 2H, 3H and 4H distances!

- Compare the calculated reattachment lengths resulted with measured values (x_R/H)!

- Compare the calculated pressure coefficient (c_p) profiles, with special attention to the correct selection of reference values.

Measured data:

Position of the reattachment point

Lid angle	Reattachment length	Error
a [°]	Xr/H	dXr/H
-2	5.82	-0.08
0	6.26	-0.1
6	8.3	-0.15
10	10.18	-0.5

Pressure coefficient (c_p) on lower wall (on the side of the step)

X/H	a=-2	a=0	a=6	a=10
-8.5	0	0.0039	0.0117	0.0088
-6.5	0	0	0.0136	0.0108
-4.5	-0.0059	-0.0048	0.0166	0.0187
-2.5	-0.0296	-0.0231	0.0214	0.0266
-0.5	-0.0642	-0.0472	0.0283	0.0512
0	-0.0859	-0.0607	0.0361	0.061
0.5	-0.0899	-0.0636	0.0331	0.06
1	-0.0899	-0.0665	0.0312	0.0571
1.5			0.0292	0.0571
2	-0.1017	-0.0742	0.0253	0.0571
2.5				0.0502
3	-0.1037	-0.0762	0.0185	0.0482
3.5	-0.083	-0.0665	0.0253
4	-0.0464	-0.0424	0.04	0.0581
4.5	0.0049	0.0077	0.0585
5	0.0494	0.0482	0.0829	0.0876
5.5	0.0771	0.0782
6	0.1037	0.1129	0.1297	0.1251
6.5	0.1205	0.1303
7	0.1275	0.1389	0.1667	0.1556
8	0.1304	0.1515	0.1989	0.1871
8.5			0.2115
9	0.1225	0.1535	0.2203	0.2117
9.5			0.231
11	0.0978	0.1477	0.2544	0.2551
12			0.2641
13	0.0751	0.1409	0.2749	0.2846
15	0.0534	0.1342	0.2924	0.3073
17	0.0385	0.1303	0.308	0.328
19.5	0.0168	0.1285	0.3265	0.3448
21.5	0.001	0.1246	0.3402	0.3596
23.5	-0.0168	0.1227	0.3528	0.3723
25.5	-0.0346	0.1227	0.3674	0.3813
27.5	-0.0494	0.1218	0.3821	0.3921
29.5	-0.0652	0.1218	0.3889	0.4011
31.5	-0.085	0.1199	0.4035	0.409
33.5	-0.1048	0.116	0.4133	0.4139
35.5	-0.1236	0.1189	0.4279	0.4198
37.5	-0.1463	0.1141	0.4347	0.4209

Pressure coefficient (c_p) on upper wall (opposite to the step)

X/H	a=-2	a=0	a=6	a=10
-5	0.0178	0.0087	0.0039	-0.0108
3	0.0306	0.0414	0.0799	0.0896
5	0.03	0.0511	0.1248	0.1536
7	0.0296	0.0598	0.1627	0.1989
9	0.0425	0.081	0.1989	0.2471
11	0.0504	0.0993	0.232	0.2816
13	0.0454	0.1118	0.2612	0.3092
15	0.0336	0.1138	0.2846	0.3338
17	0.0286	0.1206	0.308	0.3545
19	0.0148	0.1216	0.3246	0.3683
21	0.001	0.1216	0.3402	0.3821
23	-0.0158	0.1207	0.3538	0.389
25	-0.0296	0.1236	0.3713	0.3979
27	-0.0474	0.1217	0.384	0.4029
29	-0.0642	0.1208	0.3947	0.4079
31	-0.0811	0.1189	0.4055	0.4178
33	-0.1038	0.116	0.4133	0.4178
35	-0.1236	0.1179	0.4298	0.4228
37	-0.1464	0.1131	0.4396	0.4239

Task 5. (3 points)

Plot the streamlines colored by velocity magnitude, the static and total pressures as well as the turbulent kinetic energy and save images in TIF format.

Briefly describe the investigation aims, the solution methods, and the results in comparison to measurement data.

Prepare your report in PowerPoint (.PPT) format and upload to the folder specified by the practice leader!