4. Group assignment: Flow around a
cylinder at different Reynolds number
In low Reynolds number regime (Re=50…200), two-dimensional time dependent (periodic) flow takes place around cylindrical bodies. The laminar boundary layer separates on both sides of the frontal surface, producing free shear layers, the vorticity of which is being accumulated in large eddies downstream from the cylinder. The interaction between large eddies give rise to the well-known von Karman vortex sheet.
This investigation is aimed at the understanding of flow phenomenon at different Reynolds number.
The shape and proportions of the simulation domain will be chosen on the basis of Betti Bolló’s recommendations according to Fig.1. Let d¥/d = 100. u¥ velocity shall be used as boundary condition at the outer boundary.
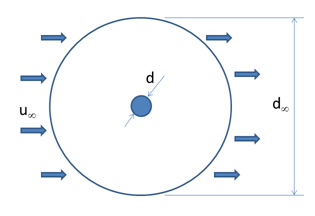
Figure 1. Geometrical
parameters and boundary conditions.
Task 1. (3 points)
Prepare the
geometrical model and a high quality inflated block-structured mesh of 6-8 thousand
elements.
Task 2. (3 points)
Chose air
as working fluid and set the value of viscosity on the way the Reynolds-number
be equal to 110! Make a pre-calculation with your coarsest mesh and check the
Courant number distribution! Set the time step size in each case corresponding
to C=1 maximum Courant number! Estimate the necessary computation time, by
assuming, that the periodic solution takes 120 * d/u¥ flow time to develop! Change mesh
sizes if necessary!
Task 3. (3 points)
Run
simulations for 3 different Reynolds numbers until reaching the periodic
solution, meanwhile monitoring lift force FL and drag FD !
Task 4. (3 points)
Calculate FD,avg (average value
of of FD), as well as f frequency and FL,rms (RMS of FL) for the periodic
solution. Evaluate the following dimensionless quantities:
![]() ,
, ![]() ,
, ![]() .
.
Please, compare your computational results with experimental data specified in Table 1!
|
Re |
50 |
70 |
90 |
110 |
130 |
150 |
170 |
Referencia |
|
St |
0.122 |
0.144 |
0.159 |
0.169 |
0.177 |
0.183 |
0.189 |
Williamson (1998) |
|
cL,rms |
0.0466 |
0.138 |
0.199 |
0.254 |
0.306 |
0.356 |
0.404 |
Norberg (2001) |
|
cD,avg |
1.45 |
1.39 |
1.36 |
1.34 |
1.33 |
1.33 |
1.33 |
Henderson
(1995) |
Table 1. Experimental data
Task 5. (3 points)
Summarize the
investigation aims and methodology as well as the results of flow pattern, time
functions and average quantities!
The report should be prepared in PowerPoint
(.PPT) file which is to be up-loaded to the personal result folder.
References:
Bolló, B, Baranyi, L., 2010. Computation of low-Reynolds number flow around a stationary circular cylinder. Proc. 7th International Conference on Mechanical Engineering, Budapest, pp. 891-896.
Henderson, R.D., 1995. Details of the drag curve near the onset of vortex shedding. Physics of Fluids 7, 2102–2104.
Norberg, C., 2001. Flow around a circular cylinder: aspects of fluctuating lift. Journal of Fluids and Structures 15, 459-469.
Williamson, C.H.K., Brown, G.L., 1998. A series in 1/√Re to represent the Strouhal-Reynolds number relationship of the cylinder wake. Journal of Fluids and Structures 12(8), 1073-1085.